Simula hipotecas con matplotlib

A continuación vemos como calcular la cuota mensual y los intereses de una hipoteca, dadas las siguientes entradas:

• 💵 Cantidad de dinero prestada.
• 📈 Porcentaje de interés anual.
• 📅 Años de la hipoteca.

El objetivo final es saber cuanto tendremos que pagar al mes durante los años que dure la hipoteca y los intereses de la misma.

Definimos una función que calcula la cuota y los intereses totales. Esta función simplemente implementa la fórmula de la amortización.

def cuota_interes(prestamo, interes, anios):
    int_mensual = interes / 1200
    num_cuotas = anios * 12
    cuota = (prestamo * int_mensual) / (1 - (1 + int_mensual) ** -num_cuotas)
    intereses = ((cuota * num_cuotas - prestamo) / prestamo) * 100
    return (cuota, intereses)

Ahora la podemos usar con los siguientes parámetros:

• 💵 Se quieren tomar prestados 100000 Euros.
• 📈 Con un 2% de interés anual.
• 📅 Durante 10 años.

Con esto podemos ver que la cuota mensual de 920 Euros y los intereses son del 10%. Es decir, después de los 10 años habremos pagado un 10% de lo que pedimos prestado.

cuota, intereses = hipoteca(100000, 2, 10)
print(f"Cuota mensual: {cuota:.2f} €")
print(f"Intereses: {intereses:.2f} %")
# Cuota mensual: 920.13 €
# Intereses: 10.42 %

Podemos realizar el cálculo para varios plazos. Desde 5 años hasta 30.

prestado = 100000
interes = 2
plazos = range(5, 31, 5)

cuotas = [hipoteca(prestado, interes, plazo)[0] for plazo in plazos]

fig, ax1 = plt.subplots(figsize=(7, 6))
ax1.set_xlabel("Plazo (años)")
ax1.set_ylabel("Cuota mensual (€)")
ax1.plot(plazos, cuotas, label="Cuota mensual (€)")
plt.title("Cuota mensual e intereses")
plt.grid(True)
plt.show()

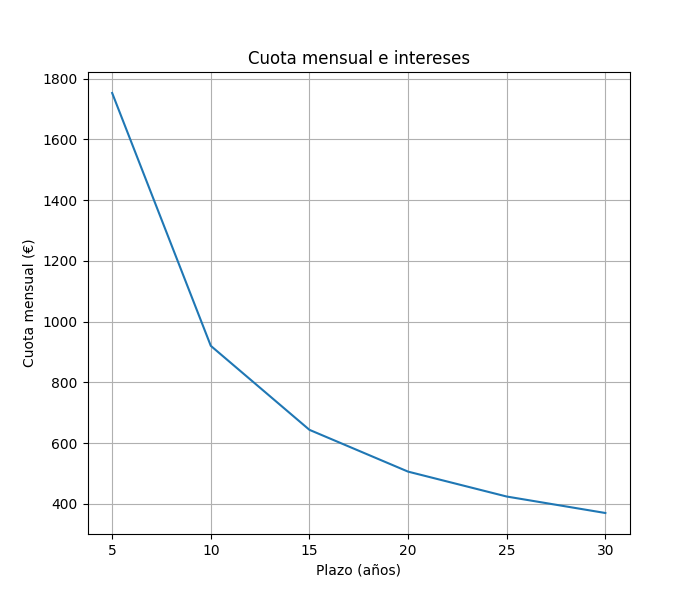
Y vemos la cuota mensual que nos quedaría en cada caso.

✏️ Ejercicios:

• Como podemos ver, la cuota mensual se reduce considerablemente cuando aumentamos el plazo de la hipoteca. Sin embargo esto tiene un efecto en los intereses que se pagan. Añade una gráfica donde se represente los intereses pagados y el plazo en años.