Simulación Monte Carlo con numpy

En este ejemplo realizamos una simulación de Monte Carlo sobre un portfolio de inversión usando numpy. Es común realizar este tipo de simulaciones en portfolios de inversión, donde existen los siguiente parámetros:

• 💶 Una cantidad de dinero inicial.
• 📈 Un retorno anual esperado pero no fijo. Varía de acuerdo a una volatilidad.
• ❓ Una volatilidad. Esta volatilidad hace variar al retorno anual.
• ⏳ Un tiempo de varios años.

El objetivo es calcular la cantidad de dinero final después del tiempo en años considerado. Si la volatilidad fuera 0 y el retorno anual fuera fijo cada año, el cálculo sería bien sencillo. Pero los mercados financieros están expuestos a incertidumbre.

Esta incertidumbre la podemos modelar con métodos de Monte Carlo, viendo los diferentes escenarios posibles. Nos dará una idea del mejor y del peor caso.

Podemos simular esta volatilidad con una distribución normal usando normal. Una vez lo tenemos, calculamos el valor_portfolio a lo largo de los años. Por último lo representamos en una gráfica.

import numpy as np
import matplotlib.pyplot as plt

def simula_portfolio(
        inicial, retorno_anual,
        volatilidad_anual, tiempo_anios,
        simulaciones):

    np.random.seed(42)
    retornos = np.random.normal(retorno_anual, volatilidad_anual, (tiempo_anios, simulaciones))
    valor_portfolio = inicial * (1 + retornos).cumprod(axis=0)

    plt.figure()
    plt.plot(valor_portfolio, alpha=0.5)
    plt.title("Simulación Monte Carlo de Portfolio")
    plt.xlabel("Año")
    plt.ylabel("Valor Portfolio (€)")
    plt.grid(True)

    mejor_caso = valor_portfolio.max(axis=1)[-1]
    peor_caso = valor_portfolio.min(axis=1)[-1]
    plt.text(tiempo_anios / 2, mejor_caso / 2,
             f'Mejor caso: {mejor_caso:.0f}€'+f'\nPeor caso: {peor_caso:.0f}€', 
             bbox=dict(facecolor='grey', alpha=0.9))

    plt.show()

Ahora podemos usar la función con los siguientes parámetros. Realizamos 100 simulaciones con 20 años como horizonte temporal. Esperamos un retorno anual del 7% con una volatilidad del 4% y usamos 100.000 Euros.

simula_portfolio(
    inicial=100_000,
    retorno_anual=0.07,
    volatilidad_anual=0.04,
    tiempo_anios=20,
    simulaciones=100)

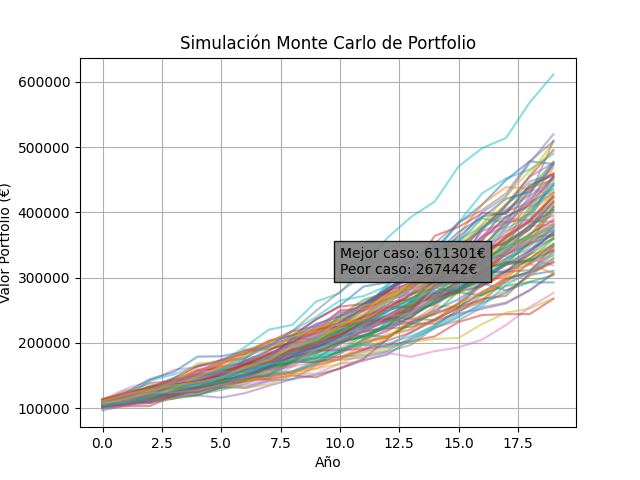
Podemos ver los diferentes resultados que obtendría este portfolio. Esto nos da una idea del mejor y del peor caso. Como puedes ver, en ninguna de nuestras simulaciones se ha perdido dinero después de los 20 años.

✏️ Ejercicios:

• Realiza la simulación usando diferentes combinaciones de retorno_anual y volatolidad_anual. Busca una combinación que de lugar a pérdidas en algunas situaciones.
• Añade una nueva representación que muestre la media de todos los escenarios posibles en una sola línea.