Introducción a Polinomios

Un polinomio es una expresión algebraica formada por la suma de varios términos. Cada término tiene un coeficiente y una o varias variables indeterminadas. Esto es un polinomio:

Podemos ver que:

• Tiene orden 2. También conocido como grado, indica la mayor potencia a la que se eleva la variable indeterminada.
• Una única variable indeterminada, x.
• Coeficientes [3, 2, 5], correspondiendo el primer elemento a la izquierda con el máximo grado. Se podría expresar también como [5, 2, 3].

Se puede por tanto definir un polinomio con la siguiente expresión, donde los coeficientes son a y x es la variable indeterminada. Nos centraremos en polinomios con una única variable indeterminada.

También podríamos definirlo de manera más genérica con la siguiente ecuación, donde n es el grado u orden.

Evaluar Polinomio

Se entiende por evaluar un polinomio a calcular su valor para un determinado valor de su variable indeterminada. Usando el polinomio anterior, podemos evaluarlo en el punto x=3 donde el resultado P(3) = 38.

Sumar y Restar Polinomios

Los polinomios también se pueden sumar y restar. Para ello, se alinean los términos semejantes, es decir, términos que tienen la misma potencia de x. Luego se suman o restan los coeficientes de casa término. Veamos un ejemplo de suma y resta usando $P(x)$ y $Q(x)$.

Multiplicar Polinomios

Para multiplicar polinomios debemos multiplicar cada término por todos los términos del segundo polinomio. Veamos un ejemplo con los mismos polinomios.

Una vez entendido el concepto de polinomio, vamos a ver cómo trabajar con ellos en Python. Tanto usando la librería estándar como con librerías externas.

Polinomios en Python

Empecemos por la representación de un polinomio en Python. Una manera común es usando listas. El polinomio anterior P(x) lo podemos representar de la siguiente manera.

polinomio = [3, 2, 5]

Como podemos ver:

• polinomio[0] hace referencia al término de mayor grado, $x^2$.
• polinomio[1] al término $x^1$.
• polinomio[2] a la constante, técnicamente $x^0 = 1$.

A continuación vamos a escribir una función que evalúa un polinomio en un punto x determinado, tal y como vimos anteriormente. Podemos hacerlo de manera naive de la siguiente manera. Simplemente reemplazamos la variable x en el polinomio.

def evaluar_naive(polinomio, x):
    return sum(c * x**i for i, c in enumerate(reversed(polinomio)))

De esta manera, si evaluamos nuestro polinomio en x=3 de la siguiente manera, obtendremos 38.

polinomio = [3, 2, 5]
print(evaluar_naive(polinomio, 3))
# 38

No obstante, aunque la función que hemos escrito es válida, se puede optimizar de la siguiente forma utilizando el método Horner. El resultado es el mismo, pero requiere de menos multiplicaciones. Esto hace que sea más rápida de ejecutar, algo que se aprecia notablemente en polinomios de grado elevado. Concretamente pasamos de una complejidad en el peor caso de O(n^2) a O(n).

def evaluar_horner(polinomio, x):
    result = 0
    for c in polinomio:
        result = result * x + c
    return result

Si no nos crees, puedes medir tu mismo el tiempo de ejecución de ambos métodos. evaluar_naive vs evaluar_horner. Vamos a crear polinomios aleatorios de grado 1 hasta grado 100 y medir el tiempo que se tarda en evaluar dicho polinomio usando ambos métodos.

x = 5
tiempos_naive, tiempos_horner = [], []
for grado in range(1, 101):
    polinomio = [random.randint(1, 100) for i in range(grado)]
    tiempos_naive.append(timeit.timeit('evaluar_naive(polinomio, x)', number=10000, globals=globals()))
    tiempos_horner.append(timeit.timeit('evaluar_horner(polinomio, x)', number=10000, globals=globals()))

plt.plot(tiempos_naive, 'bo', label="evaluar_naive")
plt.plot(tiempos_horner, 'ro', label="evaluar_horner")
plt.title("Tiempo evaluar polinimio: naive vs horner")
plt.ylabel("Tiempo 10000 ejecuciones (s)")
plt.xlabel("Grado del polinomio")
plt.legend()
plt.show()

En la siguiente figura podemos ver la diferencia. El método de horner es mucho más eficiente.

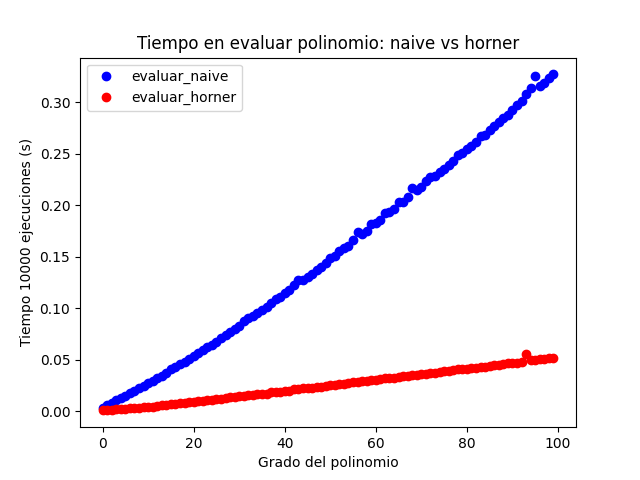
Por otro lado, sumar y restar polinomios es relativamente fácil. Sean p y q dos polinomios que queremos sumar o restar, lo podemos expresar en Python de la siguiente forma. Es importante notar que esta implementación es la más sencilla posible, y asume que el grado de ambos polinomios es igual, es decir, que la len() de los coeficientes es igual.

# resta. sólo válida para p y q del mismo grado
resta = [a - b for a, b in zip(p, q)]

# suma. sólo válida para p y q del mismo grado
suma = [a + b for a, b in zip(p, q)]

Sin embargo esta implementación es poco práctica, ya que es posible que queramos sumar polinomios de distinto grado. Para permitir esto, podemos usar zip_longest de la siguiente forma. El [::-1] simplemente invierte la lista, poniendo los elementos de derecha a izquierda.

from itertools import zip_longest

def suma_polinomios(p, q):
    return [pp+qq for pp, qq in zip_longest(p[::-1], q[::-1], fillvalue=0)][::-1]

def resta_polinomios(p, q):
    return [pp-qq for pp, qq in zip_longest(p[::-1], q[::-1], fillvalue=0)][::-1]

Por otro lado, si queremos multiplicar polinomios, podemos hacer lo siguiente. Con [0]* simplemente iniciamos una lista con longitud len(p) + len(q) - 1 llena de ceros.

def multiplica_polinomios(p, q):
    resultado = [0] * (len(p) + len(q) - 1)
    for i, pp in enumerate(p):
        for j, qq in enumerate(q):
            resultado[i + j] += pp * qq
    return resultado

Veamos un ejemplo usando p y q usando las funciones anteriormente descritas para sumar, restar y multiplicar polinomios.

p = [3, 2, 5]
q = [4, 0, 2]

print(suma_polinomios(p, q))
# [5, 3, 3, 4]

print(resta_polinomios(p, q))
# [-5, -3, -1, 2]

print(multiplica_polinomios(p, q))
# [12, 8, 26, 4, 10]

Polinomios con numpy

En el apartado anterior hemos visto cómo implementar en Python diferentes operaciones sobre polinomios. Aunque consideramos que es importante entender cómo funcionan estas operaciones y hacer estos ejemplos a modos de ejercicio, en la práctica es más común usar librerías externas. Esto nos ahorra escribir el código y es también más seguro, sobre todo cuando se trabaja con librerías ampliamente probadas como numpy.

Podemos realizar las mismas operaciones usando numpy, en concreto:

• polyval para evaluar.
• polyadd para sumar.
• polysub para restar.
• polymul para multiplicar.

p = [3, 2, 5]
q = [4, 0, 2]

print(numpy.polynomial.polynomial.polyval(3, p[::-1]))
# 38.0

print(numpy.flipud(numpy.polynomial.polynomial.polyadd(p[::-1], q[::-1])))
# [7. 2. 7.]

print(numpy.flipud(numpy.polynomial.polynomial.polysub(p[::-1], q[::-1])))
# [-1.  2.  3.]

print(numpy.flipud(numpy.polynomial.polynomial.polymul(p[::-1], q[::-1])))
# [12.  8. 26.  4. 10.]

Es importante notar que numpy considera que los coeficientes están en orden inverso a lo que sería lógico pensar. Es decir, $3x^2 + 2x + 5$ puede ser expresado de dos formas:

• [3, 2, 5]. En nuestra opinión resulta lo más lógico, al seguir el orden natural de como los polinomios se suelen ordenar.
• [5, 2, 3]. Se invirtie el orden de los coeficientes, como hace numpy.

Para que podemos comparar los resultados, usamos [::-1] y flipud para invertir el orden de los coeficientes.